LAB 2 :
MEASUREMENT & COUNTING OF CELLS USING MICROSCOPE
name: tunku syed iskandar al-qadri
matric no:111434
2.1 Ocular
Micrometer
Introduction
The first reported
measurements performed with an optical microscope were undertaken in the late
1600s by the Dutch scientist Antonie van Leeuwenhoek, who used fine grains of
sand as a gauge to determine the size of human erythrocytes. Since then,
countless approaches have been employed for measuring linear, area, and volume
specimen dimensions with the microscope (a practice known as micrometry or morphometrics),
and a wide variety of useful techniques have emerged over the past few hundred
years. To measure
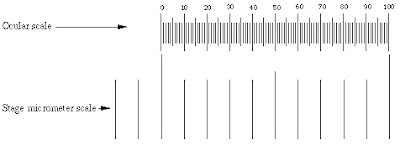
an object seen in a microscope, an ocular micrometer serves as a scale or rule.
This is simply a disc of glass upon which equally spaced divisions are etched.
The rule may be divided into 50 subdivisions, or more rarely 100 subdivisions.
To use the ocular micrometer, it must be calibrate it against a fixed and known
ruler, the stage of micrometer. Stage micrometers also come in varying lengths,
but most are 2mm long and subdivided into 0.01mm in lengths. Each objective
will need to be calibrated independently. To use, simply superimpose the ocular
micrometer onto the stage micrometer and note the relationship of the length of
the ocular to the stage micrometer. Note that at different magnifications, the
stage micrometer changes, but the ocular micrometer is fixed in dimension. In
reality, the stage micrometer is also fixed, and what is changing is the power
of the magnification of the objective.
Objective :
To measure
and count cells using a microscope
Materials
and Reagents :
·
Microscope
fitted with an ocular micrometer
Results :1.
Yeast
:
Discussion
:
Micrometry is the measurment
of microorganisms. Since microorganisms can be seen only under a microscope,
suitable scale for their measurements should be somewhere in the microscope
itself. Ocular micrometer is simply a disc of glass upon which are etched
lines. When placed in the eye piece, the ruled lines superimpose certain
distance markers on the microscope field. However, the scale on ocular
micrometer does not have any standard value. We can find out the value of one
division of this unknown scale by calibrating it with known scale. Thus actual
value of one division of ocular micrometer is found by using another known
scale, the stage micrometer.First, look through your microscope's eyepieces
and determine whether there is an ocular micrometer in place. Ocular
micrometers appear as a scale of parallel black lines similar to lines on a
ruler, often with numbers indicating sequential measures of ten lines.Calibrate the ocular micrometer if this has not been done
previously. Place a stage micrometer slide on the stage and view it through the
eyepieces, making sure that both eyepieces are focused. By rotating the
eyepiece containing the ocular micrometer and moving the stage micrometer
slide, align the two micrometers.The stage micrometer has divisions of known dimensions; use these
dimensions to determine the ocular micrometer dimensions for the objective, or
microscope lens, directly over the stage. For example, if each stage micrometer
division using a certain objective can be aligned with ten ocular micrometer
divisions, then each ocular micrometer division is one-tenth of the known stage
micrometer division length. In the example, if each stage micrometer division
measures 100 microns, then each ocular micrometer division using the objective
measures 10 microns.After calibrating the ocular micrometer for one objective, repeat
the procedure for the other microscope objectives for greatest accuracy.
Alternatively, the calibration of the other objectives can be calculated from
the measured objective calibration; however, this method can lead to error
because of variations in exact magnification. For example, a division measuring
10 microns under the 10 times magnification objective would be calculated to
measure one micron under the 100 times magnification objective. Place a slide on the microscope stage. Align the ocular
micrometer with the surface of the object on the slide to be measured by
rotating the eyepiece containing the micrometer and moving the microscope slide
with the object until the micrometer is aligned with the surface. Count the
number of micrometer divisions aligned along the surface.
Calculate the surface length by multiplying the number of measured micrometer divisions by the conversion factor determined through ocular micrometer calibration in step one. For example, if each division is one micrometer and the surface measured aligns with 10 divisions, then the surface measurement is 10 micrometers.
Calculate the surface length by multiplying the number of measured micrometer divisions by the conversion factor determined through ocular micrometer calibration in step one. For example, if each division is one micrometer and the surface measured aligns with 10 divisions, then the surface measurement is 10 micrometers.
2.2
Neubauer Chamber
Introduction
Louis-Charles
Malassez (21 September 1842–1909) was a French anatomist and histologist born in Nevers,
department of Nièvre.
Malassez is remembered for research involving histology of the blood, and is
credited for design of the hemocytometer,
a device used to quantitatively measure blood cells. In
the field of dentistry,
he described residual cells of the epithelial
root sheath in the periodontal ligament. These remaining cells are
referred to as epithelial
cell rests of Malassez (ERM).
Materials and Reagents :
·
Serial dilutions of bacteria cultures
· Neubauer an coverslip
· 70% ethanol
· Sterile Pasteur pipettes
Results :· Neubauer an coverslip
· 70% ethanol
· Sterile Pasteur pipettes
1.
Calculation :
Average of cell :
= (31 + 34 + 35 + 36 + 34 + 35 + 41 + 40 + 35 + 37 ) ÷ 10
= 35.8
Volume of square :
= 0.2 x 0.2 x 0.1
= 4 x 10-3 mm3=4 x 10-6 ml
Number of cell :
= 35.8 ÷ ( 4 x 10-6 )
= 8.95 x 106 cells/ml
Discussion :
To prepare the
counting chamber the mirror-like polished surface is carefully cleaned with
lens paper. The coverslip is also cleaned. Coverslips for counting chambers are
specially made and are thicker than those for conventional microscopy, since
they must be heavy enough to overcome the surface tension of a drop of liquid.
The coverslip is placed over the counting surface prior to putting on the cell
suspension. The suspension is introduced into one of the V-shaped wells with a
pasteur or other type of pipet. The area under the coverslip fills by capillary
action. Enough liquid should be introduced so that the mirrored surface is just
covered. The charged counting chamber is then placed on the microscope stage
and the counting grid is brought into focus at low power.Average of cell :
= (31 + 34 + 35 + 36 + 34 + 35 + 41 + 40 + 35 + 37 ) ÷ 10
= 35.8
Volume of square :
= 0.2 x 0.2 x 0.1
= 4 x 10-3 mm3=4 x 10-6 ml
Number of cell :
= 35.8 ÷ ( 4 x 10-6 )
= 8.95 x 106 cells/ml
Discussion :
It is
essential to be extremely careful with higher power objectives, since the
counting chamber is much thicker than a conventional slide. The chamber or an
objective lens may be damaged if the user is not not careful. One entire grid
on standard hemacytometers with Neubauer rulings can be seen at 40x (4x
objective). The main divisions separate the grid into 9 large squares (like a
tic-tac-toe grid). Each square has a surface area of one square mm, and the
depth of the chamber is 0.1 mm. Thus the entire counting grid lies under a
volume of 0.9 mm-cubed.Suspensions
should be dilute enough so that the cells or other particles do not overlap
each other on the grid, and should be uniformly distributed. To perform the
count, determine the magnification needed to recognize the desired cell type.
Now systematically count the cells in selected squares so that the total
count is 100 cells or so (number of cells needed for a statistically
significant count). For large cells this may mean counting the four large
corner squares and the middle one. For a dense suspension of small cells you
may wish to count the cells in the four 1/25 sq. mm corners plus the middle
square in the central square. Always decide on a specific counting patter to
avoid bias. For cells that overlap a ruling, count a cell as "in"
if it overlaps the top or right ruling, and "out" if it overlaps
the bottom or left ruling.
Here is a
way to determine a particle count using a Neubauer hemocytometer. Suppose
that you conduct a count as described above, and count 187 particles in the
five small squares described. Each square has an area of 1/25 mm-squared
(that is, 0.04 mm-squared) and depth of 0.1 mm. The total volume in each
square is (0.04)x(0.1) = 0.004 mm-cubed. You have five squares with combined
volume of 5x(0.004) = 0.02 mm-cubed. Thus you counted 187 particles in a
volume of 0.02 mm-cubed, giving you 187/(0.02) = 9350 particles per mm-cubed.
There are 1000 cubic millimeters in one cubic centimeter (same as a
milliliter), so your particle count is 9,350,000 per ml.Cells are
often large enough to require counting over a larger surface area. For
example, you might count the total number of cells in the four large corner
squares plus the middle combined. Each square has surface area of 1
mm-squared and a depth of 0.1 mm, giving it a volume of 0.1 mm-cubed. Suppose
that you counted 125 cells (total) in the five squares. You then have 125
cells per 0.5 mm-cubed, which is 250 cells/mm-cubed. Again, multiply by 1000
to determine cell count per ml (250,000).
Sometimes
you will need to dilute a cell suspension to get the cell density low enough
for counting. In that case you will need to multiply your final count by the
dilution factor. For example, suppose that for counting you had to dilute a
suspension of Chlamydomonas 10 fold. Suppose you obtained a final count of
250,000 cells/ml as described above. Then the count in the original
(undiluted) suspension is 10 x 250,000 which is 2,500,000 cells/ml.
|
Conclusion :
As the conclusion, size of the cell can be measure and the number of cell can be count by using a microscope. Size of cell that was viewed under two lens magnification for the ocular micrometer, first magnification is 40 x 10 magnification and the size is 2 divison with length of 5µm, and for 100 x 10 magnification the size is 5 division with length of 5µm also. For number of cell was counted by the Neubauer Chamber, the number of cells that obtained was 8.95 x 106 cells/ml
References :
· S. Harisha (2006). An Introduction To Practical Biotechnology (First Edition). Publish by Laxmi Publications (P) LTD. 22, Golden House, Daryaganj, New Delhi-110002.
· http://en.wikipedia.org/wiki/Hemocytometer
· http://www.microscopyu.com/articles/formulas/measurements.html
· P.D. Sharma (2007). Microbiology, 6th Reprint (Second Edition). Publised by Rakesh Kumar Rastogi for Rastogi Publications, Gangotri Shivaji Road, Meerut-250 002, New Delhi, India.
· http://www.ruf.rice.edu/~bioslabs/methods/microscopy/cellcounting.html. Created by David R. Caprette, (Rice University 11 May 00 Updated 19 Jan 07
x
LAB 2 WRITTEN BY AZIZUL
Name : Ahmad Azizul Bin Md Sadik
Matrix No : 114116
LAB 2 : MEASUREMENT & COUNTING OF CELLS USING MICROSCOPE
2.1 Ocular
Micrometer
Introduction
The first reported
measurements performed with an optical microscope were undertaken in the late
1600s by the Dutch scientist Antonie van Leeuwenhoek, who used fine grains of
sand as a gauge to determine the size of human erythrocytes. Since then,
countless approaches have been employed for measuring linear, area, and volume
specimen dimensions with the microscope (a practice known as micrometry or morphometrics),
and a wide variety of useful techniques have emerged over the past few hundred
years.
To measure
an object seen in a microscope, an ocular micrometer serves as a scale or rule.
This is simply a disc of glass upon which equally spaced divisions are etched.
The rule may be divided into 50 subdivisions, or more rarely 100 subdivisions.
To use the ocular micrometer, it must be calibrate it against a fixed and known
ruler, the stage of micrometer. Stage micrometers also come in varying lengths,
but most are 2mm long and subdivided into 0.01mm in lengths. Each objective
will need to be calibrated independently. To use, simply superimpose the ocular
micrometer onto the stage micrometer and note the relationship of the length of
the ocular to the stage micrometer. Note that at different magnifications, the
stage micrometer changes, but the ocular micrometer is fixed in dimension. In
reality, the stage micrometer is also fixed, and what is changing is the power
of the magnification of the objective.
Objective :
To measure
and count cells using a microscope
Materials
and Reagents :
·
- Microscope fitted with an ocular micrometer
- Slide micrometer
- Stained preparation of yeast and bacteria
Results :
1.
Yeast
:
Under 40 x 10 magnification.
= 2 division x 2.5 µm
= 5 µm
Under 100 x 10 magnification (oil-immersion).
= 5 division x 1.0 µm
= 5 µm
2.
Lactobacillus
:
Under 40 x 10 magnification.
Size of the sample is too small and cannot be seen.
Under 100 x 10 magnification (oil-immersion).
= 2 division x 1.0 µm
= 2 µm
Discussion
:
This basic principle is
applicable to the measurement of specimens observed in the microscope, but in
practice, it is often not possible with a compound microscope to place a ruler
in direct contact with the specimen (although this is often done in
low-magnification stereomicroscopy). Alternative mechanisms for performing
measurements at high magnifications in compound optical microscopy must be
employed, and the most common of these is the application of eyepiece reticles
in combination with stage micrometers. A majority of measurements made with
compound microscopes fall into the size range of 0.2 micrometers to 25
millimeters (the average field diameter of widefield eyepieces). Horizontal
distances below 0.2 micrometers are beneath the resolving power of the
microscope, and lengths larger than the field of view of a widefield eyepiece
are usually (and far more conveniently) measured with a stereomicroscope.
Micrometry is the measurment
of microorganisms. Since microorganisms can be seen only under a microscope,
suitable scale for their measurements should be somewhere in the microscope
itself. Ocular micrometer is simply a disc of glass upon which are etched
lines. When placed in the eye piece, the ruled lines superimpose certain
distance markers on the microscope field. However, the scale on ocular
micrometer does not have any standard value. We can find out the value of one
division of this unknown scale by calibrating it with known scale. Thus actual
value of one division of ocular micrometer is found by using another known
scale, the stage micrometer.
2.2
Neubauer Chamber
Introduction
Louis-Charles
Malassez (21 September 1842–1909) was a French anatomist and histologist born in Nevers,
department of Nièvre.
Malassez is remembered for research involving histology of the blood, and is
credited for design of the hemocytometer,
a device used to quantitatively measure blood cells. In
the field of dentistry,
he described residual cells of the epithelial
root sheath in the periodontal ligament. These remaining cells are
referred to as epithelial
cell rests of Malassez (ERM).
The hemocytometer is a device originally
designed for the counting of blood cells.
It is now also used to count other types of cells as well as other microscopic particles. The
hemocytometer was invented by Louis-Charles Malassez and consists
of a thick glass microscope
slide with
a rectangular indentation that creates a chamber. This chamber is engraved with
a laser-etched grid of
perpendicular lines. The device is carefully crafted so that the area bounded
by the lines is known, and the depth of the chamber is also known. It is
therefore possible to count the number of cells or particles in a specific
volume of fluid, and thereby calculate the concentration of cells in the fluid
overall.
hemocytometer.
Materials and Reagents :
·
Serial dilutions of bacteria cultures
·
Neubauer an coverslip
·
70% ethanol
Sterile Pasteur pipettes
Results :
Example image of cells from Neubauer Chamber at 100 x 10 magnification (oil-immersion).
1.
Calculation :
Average of cell :
= (31 + 34 + 35 + 36 + 34 + 35 +
41 + 40 + 35 + 37 ) ÷ 10
= 35.8
Volume of square :
= 0.2 x 0.2 x 0.1
= 4 x 10-3 mm3
=4 x 10-6 ml
Number of cell :
= 35.8 ÷ ( 4 x 10-6 )
= 8.95 x 106 cells/ml
Discussion :
For microbiology, cell
culture, and many applications that require use of suspensions of cells it is
necessary to determine cell concentration. One can often determine cell density
of a suspension spectrophotometrically, however that form of determination does
not allow an assessment of cell viability, nor can one distinguish cell types.
To prepare the counting chamber the mirror-like polished surface is carefully
cleaned with lens paper. The coverslip is also cleaned. Coverslips for counting
chambers are specially made and are thicker than those for conventional
microscopy, since they must be heavy enough to overcome the surface tension of
a drop of liquid. The coverslip is placed over the counting surface prior to
putting on the cell suspension. The suspension is introduced into one of the
V-shaped wells with a pasteur or other type of pipet. The area under the
coverslip fills by capillary action. Enough liquid should be introduced so that
the mirrored surface is just covered. The charged counting chamber is then
placed on the microscope stage and the counting grid is brought into focus at
low power.
It is essential to be extremely careful with higher power
objectives, since the counting chamber is much thicker than a conventional
slide. The chamber or an objective lens may be damaged if the user is not not
careful. One entire grid on standard hemacytometers with Neubauer rulings can
be seen at 40x (4x objective). The main divisions separate the grid into 9
large squares (like a tic-tac-toe grid). Each square has a surface area of one
square mm, and the depth of the chamber is 0.1 mm. Thus the entire counting
grid lies under a volume of 0.9 mm-cubed.
Suspensions should be dilute enough so that the cells or
other particles do not overlap each other on the grid, and should be uniformly
distributed. To perform the count, determine the magnification needed to
recognize the desired cell type. Now systematically count the cells in selected
squares so that the total count is 100 cells or so (number of cells needed for
a statistically significant count). For large cells this may mean counting the
four large corner squares and the middle one. For a dense suspension of small
cells you may wish to count the cells in the four 1/25 sq. mm corners plus the
middle square in the central square. Always decide on a specific counting
patter to avoid bias. For cells that overlap a ruling, count a cell as
"in" if it overlaps the top or right ruling, and "out" if
it overlaps the bottom or left ruling.
Here is a way to determine a particle count using a Neubauer
hemocytometer. Suppose that you conduct a count as described above, and count
187 particles in the five small squares described. Each square has an area of
1/25 mm-squared (that is, 0.04 mm-squared) and depth of 0.1 mm. The total volume
in each square is (0.04)x(0.1) = 0.004 mm-cubed. You have five squares with
combined volume of 5x(0.004) = 0.02 mm-cubed. Thus you counted 187 particles in
a volume of 0.02 mm-cubed, giving you 187/(0.02) = 9350 particles per mm-cubed.
There are 1000 cubic millimeters in one cubic centimeter (same as a
milliliter), so your particle count is 9,350,000 per ml.
Cells are often large enough to require counting over a
larger surface area. For example, you might count the total number of cells in
the four large corner squares plus the middle combined. Each square has surface
area of 1 mm-squared and a depth of 0.1 mm, giving it a volume of 0.1 mm-cubed.
Suppose that you counted 125 cells (total) in the five squares. You then have
125 cells per 0.5 mm-cubed, which is 250 cells/mm-cubed. Again, multiply by
1000 to determine cell count per ml (250,000).
Sometimes you will need to dilute a cell suspension to get
the cell density low enough for counting. In that case you will need to
multiply your final count by the dilution factor. For example, suppose that for
counting you had to dilute a suspension of Chlamydomonas 10 fold. Suppose you
obtained a final count of 250,000 cells/ml as described above. Then the count
in the original (undiluted) suspension is 10 x 250,000 which is 2,500,000
cells/ml.
Conclusion :
References :
- S. Harisha (2006). An Introduction To Practical Biotechnology (First Edition). Publish by Laxmi Publications (P) LTD. 22, Golden House, Daryaganj, New Delhi-110002.
- http://en.wikipedia.org/wiki/Hemocytometer
- http://www.microscopyu.com/articles/formulas/measurements.html
- P.D. Sharma (2007). Microbiology, 6th Reprint (Second Edition). Publised by Rakesh Kumar Rastogi for Rastogi Publications, Gangotri Shivaji Road, Meerut-250 002, New Delhi, India.
- http://www.ruf.rice.edu/~bioslabs/methods/microscopy/cellcounting.html. Created by David R. Caprette, (Rice University 11 May 00 Updated 19 Jan 07



No comments:
Post a Comment